An introduction to the OOPN theory

OOPN is considered as an Object-oriented mathematical machine with:

• Structure
  • set of classes specifying inscance variables nad methods.
• Behavior
  • State - defined by states of all existing objects.
  • Evolution rules - conditions of occurrences of events and effect of the events. We distinguish four kinds of events:

     

    A - change of an object state without interaction with other objects.

    N - creation of a new object.

    F - creation of a new instance of a method.

    J - termination of a method instance.

    Each event comprise garbage collecting - deletion of unreachable objects.

The OOPN Structure

 

An object-oriented Petri net is a triple $(\Sigma,c_{0},oid_{0})$ where $\Sigma$ is a system of classes, c₀ an initial class, and oid₀ the name of an initial object from c₀.

$\Sigma$ contains sets of OOPN elements which constitute classes. It comprises constants CONST, variables VAR, net elements (such as places P and transitions T), class elements (such as object nets ONET, method nets MNET, synchronous ports SYNC, and message selectors MSG), classes CLASS, object identifiers OID, and method net instance identifiers MID. We denote $NET = ONET \cup MNET$ and $ID = OID \cup MID$. The universe U of an OOPN contains (nested) tuples of constants, classes, and object identifiers. Let $BIND = \{ b \mid b: \textit{VAR} \longrightarrow U \}$ be the set of all bindings of variables.

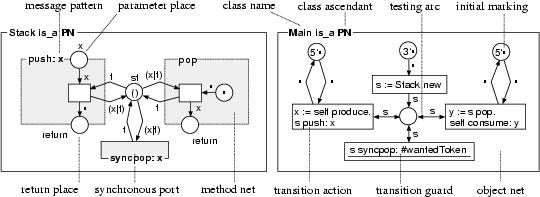
Object nets consist of places and transitions. Every place has some initial marking. Every transition has conditions (i.e. inscribed testing arcs), preconditions (i.e. inscribed input arcs), a guard, an action, and postconditions (i.e. inscribed output arcs). Method nets are similar to object nets but, in addition, each of them has a set of parameter places and a return place. Method nets can access places of the appropriate object nets in order to allow running methods to modify states of objects which they are running in.

Synchronous ports are special transitions which cannot fire alone but only dynamically fused to some other transitions which ``activate'' them from their guards via message sending. Every synchronous port embodies a set of conditions, preconditions, and postconditions over places of the appropriate object net, and further a guard, and a set of parameters. Parameters of an activated port s can be bound to constants or unified with variables defined on the level of the transition or port that activated s.

A class is specified by an object net (an element of ONET), a set of method nets (a subset of MNET), a set of synchronous ports (a subset of SYNC), and a set of message selectors (a subset of MSG) corresponding to its method nets and ports. Object nets describe possible independent activities of particular objects, method nets reactions of objects to messages sent to them from outside, and ports allow for remotely testing and changing states of objects in an atomic way. The inheritance mechanism of OOPNs allows for an incremental specification of classes. Inherited methods and synchronous ports can be redefined and new methods and synchronous ports can be added. A similar mechanism applies for object net places and transitions.

The Dynamic Behaviour of OOPNs

The dynamic behaviour of OOPNs corresponds to the evolution of a system of objects. An object is a system of net instances which contains exactly one instance of the appropriate object net and a set of currently running instances of method nets. Every net instance entails its identifier $id \in ID$ and a marking of its places and transitions. A marking of a place is a multiset of elements of the universe U. A transition marking is a set of invocations. Every invocation contains an identifier $id \in MID$ of the invoked net instance and a stored binding $b \in BIND$ of the input variables of the appropriate transition.

A state of a running OOPN has the form of a marking. To allow for the classical Petri net-way of manipulating markings, they are represented as multisets of token elements. In the case of a transition marking, the identifier of the invoked method net instance is stored within the appropriate binding in a special (user-invisible) variable $\Mid$. Thus a formal compatibility of place and transition markings is achieved and it is possible to define a token element as a triple consisting of the identifier of the net instance it belongs to, the appropriate place or transition, and an element of the universe or a binding. Then we can say for a marking M that:

$$M \in [(ID \times P \times U) \cup (ID \times T \times BIND)]^{MS}.$$

A step from a marking of an OOPN into another marking can be described as the so-called event. Such an event is a 4-tuple

E = (e,id,t,b)

including (1) its type e, (2) the identifier $id \in ID$ of the net instance it takes place in, (3) the transition $t \in T$ it is statically represented by, and (4) the binding tree b containing the bindings used on the level of the invoked transition as well as within all the synchronous ports (possibly indirectly) activated from that transition. There are four kinds of events according to the way of evaluating the action of the appropriate transition: A - an atomic action involving trivial computations only, N - a new object instantiation via the message new, F - an instantiation of a Petri-net described method, and J - terminating a method net instance. If an enabled event E occurs in a marking M and changes it into a marking M', we call this a step and denote it by

M [E> M'.

Each step comprise garbage collecting - deletion of net instances which are not reachable (by references) from the initial object. For a given OOPN, its initial marking M₀ corresponds to a single, initially marked object net instance from the initial class c₀ identified as oid₀.