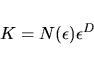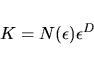Next: Hausdorffova dimenze a soběpodobnost
Up: Fraktální geometrie
Previous: Geometricky hladké útvary
Z předchozí podkapitoly vyplývá závěr, že pro běžné útvary
vystačíme s dimenzemi 0, 1, 2 nebo 3. Proto bylo poměrně velkým
překvapením, když byly objeveny zvláštní geometrické útvary, pro
které toto rozdělení na celočíselné dimenze není dostatečné. Některé
tyto útvary nejsou jen abstraktní objekty vzniklé fantazií matematiků,
ale mají své vzory přímo v přírodě.
Klasický příklad takového útvaru je břeh nějaké řeky či potoka, nebo
pobřeží nějakého reálného ostrova. Můžeme zkusit vypočítat délku
pobřeží tohoto ostrova. Je-li linie pobřeží zobrazena na nějaké mapě
(nebo leteckém snímku), má tato mapa určité měřítko, například
1: 1 000 000. Pomocí kružítka můžeme (krokováním) délku pobřeží
přibližně zjistit a přepočítat na kilometry, protože známe měřítko
mapy. Jestliže bude kružítko roztaženo tak, aby vzdálenost mezi jeho
hroty byla jeden centimetr a měřítko mapy je 1 : 1 000 000, pak
to znamená, že při jednom kroku kružítka se na mapě posuneme o
1 000 000 centimetrů, což po přepočtu dává deset kilometrů.
Dostaneme-li však k dispozici přesnější mapu, která má měřítko
například 1: 10 000 a budeme-li opět měřit délku toho samého
úseku pobřeží, dostaneme délku odlišnou - větší. To znamená, že
se změnou měřítka se změnila délka toho samého objektu - v našem
případě pobřeží. Důvod se zdá být jasný - při zmenšení měřítka vidíme
i detaily pobřeží, které nebyly na mapě s větším měřítkem viditelné.
Samozřejmě, že při cestě pěšky okolo ostrova bude délka ještě
větší, ovšem za předpokladu, že půjdeme přesně na hranici pobřeží a
nebudeme si cestu zkracovat. Se zmenšujícím se měřítkem by délka dále
rostla, a při délce měření blížící se limitně k nule, by délka rostla
dokonce až do nekonečna. Z toho vyplývá zajímavý fakt, že ostrov o
konečné ploše má nekonečnou délku pobřeží.
Výše uvedený příklad není pouhou myšlenkovou abstrakcí, ale vyskytl se
reálně při měření obvodu ostrova Korsiky. Čím byla větší přesnost tohoto
měření, tím větší byla naměřená délka. Tato skutečnost nebyla dlouhou
dobu známa, a proto se délky státních hranic lišily až o násobky
očekávaných délek. V dnešní době se v moderních atlasech délka hranic
většinou ani neuvádí.
Obvod ostrova Korsiky měřil Richardson, který také jako první
zjistil, že obvod ostrova je závislý na délce tyče, kterou se
měří. Richardson také empiricky odvodil následující vztah:
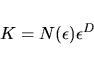 |
(1.9) |
kde K je délka celkového počtu
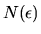 úseček nutných k
aproximaci (pokrytí) dané křivky. Délka pobřeží se ukázala být závislá
na konstantě D, jejíž význam si však Richardson nedokázal vysvětlit. Až
Benoit B. Mandelbrot dokázal souvislost této konstanty a
Hausdorffovy dimenze - viz dále.
Také délka řek se musí měřit odlišným způsobem, než jaký byl běžně
používán. Můžeme změřit délku řeky tak, že postupně změříme délku
pravého a levého břehu a výslednou vzdálenost zprůměrujeme. Jak však již
víme, v tomto případě by se při velmi přesném měření délka řek
pohybovala v astronomických jednotkách a limitně by se blížila
nekonečnu. Jak však intuitivně víme, délka řeky nemůže být nekonečná,
protože jestliže na řece poplujeme konstantní rychlostí, určitě
doplujeme na konec řeky v konečném čase. Je tedy nutné měřit například
po pevně daných krocích, nebo přímo v toku řeky.
Také plocha některých objektů v přírodě, které mají konečný objem, může
být nekonečná (nebo až o několik řádů větší, než bychom zprvu
očekávali). Například povrch planety je teoreticky nekonečný. Zdálky
vypadá planeta jako dokonalá koule (či rotační elipsoid). Při určitém
přiblížení rozeznáme vrcholky hor a velká údolí. Při dalším příblížení
zjistíme, že každá hora je velmi členitá a její plocha je obdobně
členitá jako povrch celé planety. Každý kámen potom vypadá jako celá
hora, ale je mnohem menší. S touto změnou měřítka můžeme pokračovat dále
až do subatomárních struktur.
Obrovská je i plocha plic či lidského mozku při relativně malém objemu.
Ve všech těchto případech jde o praktickou aplikaci fraktálů v přírodě,
kde obecně platí princip úspornosti.
úseček nutných k
aproximaci (pokrytí) dané křivky. Délka pobřeží se ukázala být závislá
na konstantě D, jejíž význam si však Richardson nedokázal vysvětlit. Až
Benoit B. Mandelbrot dokázal souvislost této konstanty a
Hausdorffovy dimenze - viz dále.
Také délka řek se musí měřit odlišným způsobem, než jaký byl běžně
používán. Můžeme změřit délku řeky tak, že postupně změříme délku
pravého a levého břehu a výslednou vzdálenost zprůměrujeme. Jak však již
víme, v tomto případě by se při velmi přesném měření délka řek
pohybovala v astronomických jednotkách a limitně by se blížila
nekonečnu. Jak však intuitivně víme, délka řeky nemůže být nekonečná,
protože jestliže na řece poplujeme konstantní rychlostí, určitě
doplujeme na konec řeky v konečném čase. Je tedy nutné měřit například
po pevně daných krocích, nebo přímo v toku řeky.
Také plocha některých objektů v přírodě, které mají konečný objem, může
být nekonečná (nebo až o několik řádů větší, než bychom zprvu
očekávali). Například povrch planety je teoreticky nekonečný. Zdálky
vypadá planeta jako dokonalá koule (či rotační elipsoid). Při určitém
přiblížení rozeznáme vrcholky hor a velká údolí. Při dalším příblížení
zjistíme, že každá hora je velmi členitá a její plocha je obdobně
členitá jako povrch celé planety. Každý kámen potom vypadá jako celá
hora, ale je mnohem menší. S touto změnou měřítka můžeme pokračovat dále
až do subatomárních struktur.
Obrovská je i plocha plic či lidského mozku při relativně malém objemu.
Ve všech těchto případech jde o praktickou aplikaci fraktálů v přírodě,
kde obecně platí princip úspornosti.




Next: Hausdorffova dimenze a soběpodobnost
Up: Fraktální geometrie
Previous: Geometricky hladké útvary
Tisnovsky Pavel
1999-05-30