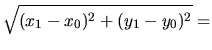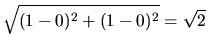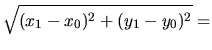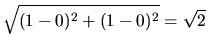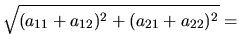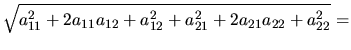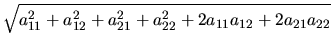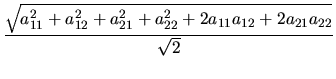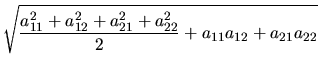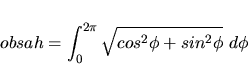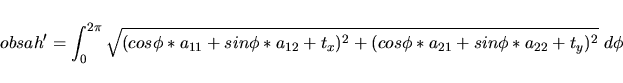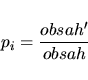Next: Uniformní rozdělení pravděpodobností
Up: Výpočet pravděpodobnosti jednotlivých transformací
Previous: Výpočet pravděpodobnosti z poměru
Tato metoda využívá pro výpočet pravděpodobnosti koeficient zkrácení
úsečky. Pro zjednodušení výpočtů neuvažujeme libovolnou úsečku. Výpočet
se provede pro úsečku, která vychází z bodu [0,0] do bodu [1,1]. V
tomto případě lze vzorec pro výpočet pravděpodobnosti i-té transformace
přímo odvodit.
Zadané hodnoty:
| x0 |
= |
0 |
(4.68) |
| y0 |
= |
0 |
(4.69) |
| x1 |
= |
1 |
(4.70) |
| y1 |
= |
1 |
(4.71) |
Hodnoty vypočtené po aplikaci transformace:
| x0' |
= |
a11x0+a12y0+tx |
(4.72) |
| y0' |
= |
a21x0+a22y0+ty |
(4.73) |
| x1' |
= |
a11x1+a12y1+tx |
(4.74) |
| y1' |
= |
a21x1+a22y1+ty |
(4.75) |
Do těchto vztahů dosadíme hodnoty
x0,x1,y0 a y1:
| x0' |
= |
a110+a120+tx=tx |
(4.76) |
| y0' |
= |
a210+a220+ty=ty |
(4.77) |
| x1' |
= |
a111+a121+tx=a11+a12+tx |
(4.78) |
| y1' |
= |
a211+a221+ty=a21+a22+ty |
(4.79) |
Délka netransformované úsečky je rovna:
| d |
= |
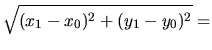 |
(4.80) |
| |
= |
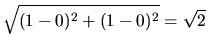 |
(4.81) |
Délka transformované úsečky se vypočítá pomocí transformovaných bodů:
| d' |
= |
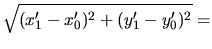 |
(4.82) |
| |
= |
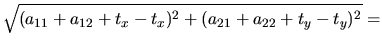 |
(4.83) |
| |
= |
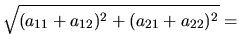 |
(4.84) |
| |
= |
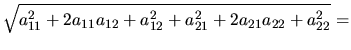 |
(4.85) |
| |
= |
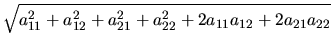 |
(4.86) |
Pravděpodobnost dané transformace se vypočte jako podíl těchto dvou délek:
| pi |
= |
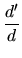 |
(4.87) |
| pi |
= |
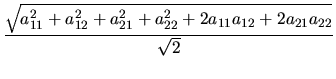 |
(4.88) |
| pi |
= |
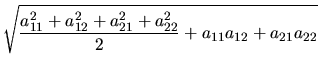 |
(4.89) |
Tato metoda je jednoduchá pro výpočet, ale má některé nevýhody. První
nevýhodou je, že úsečka je jednorozměrná. To znamená, že pravděpodobnost
je přímo úměrná změně délce úsečky. Přesnější výsledky dávají metody,
které pravděpodobnost počítají jako změnu obsahu nějakého útvaru.
Rozdíl je tedy v lineárním či kvadratickém poměru. Například
transformace, která provede zmenšení objektu na polovinu bude mít
pravděpodobnost rovnu
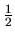 .
Budeme-li však pravděpodobnost
počítat některou z předchozích metod, vyjde tato pravděpodobnost rovna
.
Budeme-li však pravděpodobnost
počítat některou z předchozích metod, vyjde tato pravděpodobnost rovna
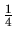 .
Tato hodnota je přesnější, neboť základní objekt
pokryjeme čtyřmi objekty, z nichž každý je zmenšený na polovinu.
Druhou nevýhodou této metody je, že počítá zkrácení jen jedné pevně dané
úsečky. To může způsobit chyby v případě, že daná transformace změní
tvar tělesa v jiném směru, než jaký má tato úsečka. Pro ilustraci můžeme
zadat transformaci, která nejprve otočí objekt o 45 stupňů doprava,
potom provede horizontální změnu měřítka a následně objekt otočí o 45
stupňů doleva. Můžeme se přesvědčit, že zatímco tvar objektu se změní,
délka úsečky zůstane konstantní.
Bylo by tedy vhodnější, aby se spočítala změna délky různě orientovaných
úseček. Problém nastává v případě, že chceme spočítat výslednou
pravděpodobnost. Poměr zkrácení všech úseček by se měl zprůměrovat,
přičemž se musí použít geometrický průměr, ne aritmetický.
Pro co nejpřesnější výpočet můžeme jednu úsečku nahradit vektorem s
pevně danou délkou, který se otáčí okolo středu. Při jedné otočce
vektoru se tedy vypočítá obsah kružnice o poloměru rovném délce vektoru.
Musí se tedy provést integrace, aby se zjistil obsah této kružnice:
.
Tato hodnota je přesnější, neboť základní objekt
pokryjeme čtyřmi objekty, z nichž každý je zmenšený na polovinu.
Druhou nevýhodou této metody je, že počítá zkrácení jen jedné pevně dané
úsečky. To může způsobit chyby v případě, že daná transformace změní
tvar tělesa v jiném směru, než jaký má tato úsečka. Pro ilustraci můžeme
zadat transformaci, která nejprve otočí objekt o 45 stupňů doprava,
potom provede horizontální změnu měřítka a následně objekt otočí o 45
stupňů doleva. Můžeme se přesvědčit, že zatímco tvar objektu se změní,
délka úsečky zůstane konstantní.
Bylo by tedy vhodnější, aby se spočítala změna délky různě orientovaných
úseček. Problém nastává v případě, že chceme spočítat výslednou
pravděpodobnost. Poměr zkrácení všech úseček by se měl zprůměrovat,
přičemž se musí použít geometrický průměr, ne aritmetický.
Pro co nejpřesnější výpočet můžeme jednu úsečku nahradit vektorem s
pevně danou délkou, který se otáčí okolo středu. Při jedné otočce
vektoru se tedy vypočítá obsah kružnice o poloměru rovném délce vektoru.
Musí se tedy provést integrace, aby se zjistil obsah této kružnice:
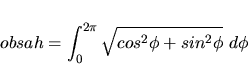 |
(4.90) |
Poté se vypočte obsah objektu, který vznikne rotací vektoru po
transformaci. Obecně musí vyjít elipsa:
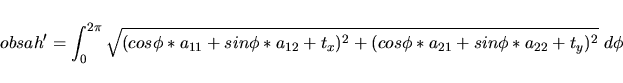 |
(4.91) |
Výsledná pravděpodobnost se potom opět vypočte z poměru těchto dvou ploch:
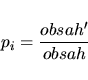 |
(4.92) |
Jak je z předchozích vztahů vidět, tento způsob výpočtu pravděpodobnosti
je velmi komplikovaný a časově náročný. Přitom neodstraňuje základní
nevýhodu této metody, tj. lineární závislost pravděpodobnosti na změně
měřítka.




Next: Uniformní rozdělení pravděpodobností
Up: Výpočet pravděpodobnosti jednotlivých transformací
Previous: Výpočet pravděpodobnosti z poměru
Tisnovsky Pavel
1999-05-30