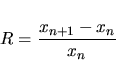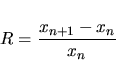Model populačního růstu

Nechť x₀ je velikost první (inicializační) populace a x_n je hodnota populace po n rocích. Velikost růstu R je relativní přírustek za jeden rok:

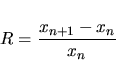$$R=\frac{x_{n+1}-x_n}{x_n}$$ (2.2)

Jestliže je R konstantní (r), pak je dynamický zákon následující:

x_n+1=f(x_n)=(1+r)x_n (2.3)

Po n rocích je velikost populace rovna:

x_n=(1+r)ⁿx₀ (2.4)

Aby byl tento exponenciální růst limitován, R se mění s velikostí populace, R tedy závisí na velikosti populace:

R=r(1-x_n) (2.5)

Čím vyšší je velikost populace x_n, tím nižší je přírustek a naopak. Parametr r se nazývá parametr růstu. Jestliže je x_n<1, populace se neustále zvětšuje. Zvětšování se zastaví, až dosáhne hodnoty x_n=1. Dynamický zákon má potom tvar:

x_n+1 = f(x_n)=(1+r)x_n-rx_n² (2.6)

x_n+1 = f(x,n)=x_n+rx_n(1-x_n) (2.7)

 

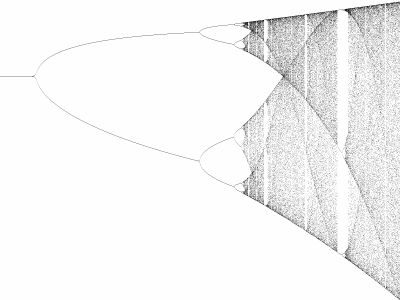
Figure: Bifurkační diagram

Pouze pro dvě hodnoty x₀ je systém stabilní. Tyto hodnoty jsou 0 a 1. Liší-li se počáteční hodnota od nuly jen nepatrně, systém se po několika iteracích vzdálí od počáteční hodnoty. To znamená, že hodnota 0 je nestabilní. Atraktorem systému je pro r<2.57 pouze 1. Pro r>2.57 (257 procent) je systém chaotický. To znamená, že i když je hodnota generována deterministickým vzorcem, stav systému nelze do budoucnosti žádným způsobem předpovědět. Nakreslíme-li graf, ve kterém budeme na vodorovnou osu vynášet hodnoty r a na svislou osu dosažené hodnoty populace, získáme takzvaný bifurkační diagram (viz obrázek). Pro některé hodnoty nabývá systém pouze jednoho stavu, pro některé dvou stavů atd, ale pro některé hodnoty je celý systém chaotický, jak je ostatně vidět na obrázku. Tento diagram je fraktálem, protože je soběpodobný.