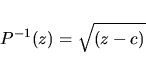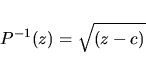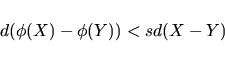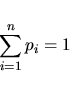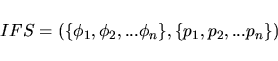Typy transformací v systému iterovaných funkcí

Systém IFS je tvořen množinou transformací, které mohou mít různou podobu. Jednou z těchto transformací je inverzní vzorec pro Juliovu množinu:

P(z)=z²+c (3.8)

Inverzní vzorec má potom tvar:

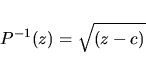$$P^{-1}(z)=\sqrt{(z-c)}$$ (3.9)

Řešením tohoto vzorce jsou vždy dvě hodnoty (dva kořeny rovnice), proto se jedná o IFS se dvěma transformacemi.

 

Figure: Inverzní Juliova množina jako IFS

Pro běžné použití IFS však uvažujeme pouze omezenou množinu transformací. Tyto transformace označujeme pojmem afinní transformace. Afinní transformace mají tu vlastnost, že jsou lineární, to znamená, že při aplikaci takovéto transformace na úsečku vyjde rovněž úsečka. Použití tohoto typu transformací značně zjednoduší všechny výpočty, které budeme provádět s IFS množinou. Transformace musí splňovat ještě jednu podmínku, musí být kontrakcemi. To znamená, že po aplikaci transformace na libovolné dva body, bude nová vzdálenost bodů menší než původní vzdálenost bodů. Tato vlastnost nám mimo jiné zaručuje, že atraktorem množiny IFS nikdy nebude nekonečno. Transformace v Euklidově prostoru definujeme takto:

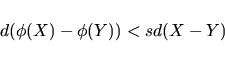$$d(\phi(X)-\phi(Y))<sd(X-Y)$$ (3.10)

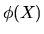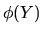kde d(X) je Euklidova metrika, X a Y jsou libovolné dva body a $\phi(X)$ a $\phi(Y)$ jsou transformované body. Podle velikosti koeficientu s pak určujeme typ transformace jako:

• s<1 : 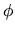$\phi$ je zmenšení (kontrakce)
• s=1 : 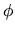$\phi$ je symetrie
• s>1 : 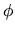$\phi$ je zvětšení (extrakce)

Z hlediska těchto vlastností není důležitá poloha transformované množiny. Za identické se například pokládají dvě stejně dlouhé úsečky, ať leží kdekoli. K množině zobrazení 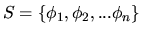$S=\{\phi_1,\phi_2,...\phi_n\}$ náleží ještě množina pravděpodobností 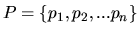$P=\{p_1,p_2,...p_n\}$, p_i>0. Pro tyto pravděpodobnosti musí platit podmínka jednotkového součtu:

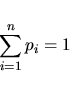$$\sum_{i=1}^np_i=1$$ (3.11)

Množina S je průměrně kontraktivní, pokud platí podmínka:

s₁^p1.s₂^p2...s_n^pn<1 (3.12)

Platí-li předchozí vztah, potom uspořádanou dvojici

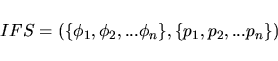$$IFS=(\{\phi_1,\phi_2,...\phi_n\},\{p_1,p_2,...p_n\})$$ (3.13)

nazveme systémem iterovaných funkcí - IFS.