



Next: Model populačního růstu
Up: Dynamické systémy s fraktální
Previous: Dynamické systémy s fraktální
Při studiu populačního růstu se došlo k závěru, že populační růst v
určitém časovém období (například roce) závisí na populačním růstu v
předchozím časovém období (relativně k celkové části populace).
Populační růst klesá, jakmile celková část populace dosáhne určité
hodnoty X. Tento proces je nelineární a protože jde o stav vyvíjející
se v čase, jde i o proces dynamický. Pro tento systém se používá název Verhulstův proces.
Pro hodnotu růstu, který je menší než 200 procent, se po určité době
stav populace ustálí na hodnotě X a nenastávají žádné odchylky.
Hodnota X je tedy pro tuto hodnotu růstu atraktorem.
Jestliže hodnota růstu dosahuje 200 procent, hodnoty X se nikdy
nedosáhne. Systém osciluje mezi hodnotou, která je menší než X a
hodnotou, která je větší než X. Existují tedy dvě velikosti populace,
které se každý rok vyměňují. Tyto dvě hodnoty jsou atraktorem, který je
periodický.
Jestliže hodnota růstu dosáhne 245 procent, nastává oscilace mezi čtyřmi
stavy. Hodnoty X se samozřejmě nikdy nedosáhne, tyto čtyři stavy jsou
tedy atraktorem.
Pro hodnoty větší než 245 procent nastává postupně oscilace mezi osmi,
šestnácti, dvaatřiceti ... stavy.
Zajímavý efekt nastane, je-li hodnota růstu větší než 257 procent. Pro
tyto hodnoty se systém stává chaotický, to znamená, že velikost populací
v následujících letech je nepředvídatelná.
Vzdálenost parametrů intervalů, kde jsou periody stabilní (tedy
například oněch 245 procent), se nazývá Feigenbaumovo číslo. Toto
číslo (přesněji řečeno konstanta) je univerzální, stejně jako například
číslo 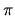 nebo e. Označuje se
nebo e. Označuje se 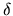 a má přibližnou hodnotu
a má přibližnou hodnotu
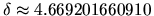 .
.




Next: Model populačního růstu
Up: Dynamické systémy s fraktální
Previous: Dynamické systémy s fraktální
Tisnovsky Pavel
1999-05-30







