



Next: Teorém pevného bodu
Up: Systém iterovaných funkcí IFS
Previous: Úvod
Při definici IFS se vychází z teorie pevných bodů, která je aplikací
věty o Banachově pevném bodu:
Nechť U je metrický prostor s metrikou d a f je funkce mapující:
přičemž 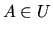 .
Jestliže má funkce bod x0 takový, že platí:
.
Jestliže má funkce bod x0 takový, že platí:
pak se x0 nazývá pevný bod.
Potom platí následující věta:
Jestliže je A podmnožinou množiny U a f je taková funkce, která mapuje
množinu A do sebe sama, přičemž existuje určitá konstanta 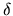 (nazývaná
kontrakční faktor), pro kterou platí
(nazývaná
kontrakční faktor), pro kterou platí
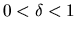 ,
potom:
,
potom:
![\begin{displaymath}d[f(x),f(y)]<\delta.d[x,y]
\end{displaymath}](img86.gif) |
(3.3) |
a funkce f se nazývá kontrakce.
Poznámka: d v našem případě znamená vzdálenost, ať už jakkoliv
definovanou. Z toho vyplývá, že IFS mohou být definovány nad jakýmkoliv
prostorem, který má definován pojem vzdálenosti. Například pro Euklidovu
metriku platí:
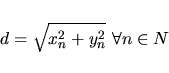 |
(3.4) |
Po k iteracích potom platí:
![\begin{displaymath}d[f^{(k)}(x),x_0]<\delta^k.d[x,x_0]
\end{displaymath}](img88.gif) |
(3.5) |
Jestliže vezmeme v úvahu tu skutečnost, že kontrakční faktor leží v
rozsahu od nuly do jedné, potom limita pro k iterací, pro k blížící
se k nekonečnu, je rovna nule, tedy:
![\begin{displaymath}\lim_{k\rightarrow \infty} d[f^{(k)}(x),x_0]=0
\end{displaymath}](img89.gif) |
(3.6) |
Dá se dokázat věta tvrdící, že pevný bod pro danou kontrakci existuje
právě jeden. Touto problematikou se zabývá takzvaný teorém pevného
bodu.




Next: Teorém pevného bodu
Up: Systém iterovaných funkcí IFS
Previous: Úvod
Tisnovsky Pavel
1999-05-30
![\begin{displaymath}d[f(x),f(y)]<\delta.d[x,y]
\end{displaymath}](img86.gif)




![\begin{displaymath}d[f(x),f(y)]<\delta.d[x,y]
\end{displaymath}](img86.gif)
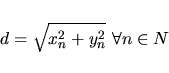
![\begin{displaymath}d[f^{(k)}(x),x_0]<\delta^k.d[x,x_0]
\end{displaymath}](img88.gif)
![\begin{displaymath}\lim_{k\rightarrow \infty} d[f^{(k)}(x),x_0]=0
\end{displaymath}](img89.gif)



