Next: Nekonečně členité útvary
Up: Fraktální geometrie
Previous: Definice fraktální geometrie
Běžná tělesa a útvary v našem okolí se dají popsat nebo zobrazit jako
jistý konečný počet parametrů, které tato tělesa charakterizují.
Pro základní geometrické tvary, například pro krychli, kouli, válec,
prstenec, úsečku, přímku či rovinu, známe vzorce a vztahy, ze kterých
můžeme vypočítat jejich geometrické charakteristiky, například
délku, plochu či objem. Jako samozřejmost přitom bereme to, že
výsledek je vždy stejný, i když počítáme v libovolných jednotkách. Je
například nepodstatné, zda je poloměr koule zadaný v milimetrech
či kilometrech; objem koule či její povrch vyjde vždy stejný (samozřejmě
při přepočtu na stejné jednotky).
Tyto veličiny (objem, povrch atd.) můžeme spočítat i pro poněkud
složitější útvary, které vzniknou kombinací konečného počtu
elementárních útvarů. Lze třeba spočítat délku Bézierovy křivky
nebo objem láhve vzniklé rotací této křivky okolo osy rotace.
Výsledky jsou opět nezávislé na použitých jednotkách. Všechny tyto
útvary mají jednu společnou vlastnost. Každému útvaru můžeme
přiřadit jisté celé číslo, které nazýváme počet rozměrů nebo
také dimenze daného útvaru.
Takže úsečka, přímka či jiná křivka (například parabola,
sinusovka či Bézierova křivka) má dimenzi rovnu 1. To znamená, že
je jednorozměrná a tudíž poloha bodu je na ní definována pouze
jedním číslem - souřadnicí. Například polohu bodu na sinusovce lze
vyjádřit jako:
kde t je jediný parametr, který jednoznačně definuje polohu
bodu na sinusovce. Hodnota x potom přímo udává polohu tohoto bodu.
To, že má křivka dimenzi rovnu jedné neznamená, že je
zobrazována v jednorozměrném prostoru. Dimenze udává jen počet
parametrů, které jsou nutné pro definování bodu na křivce. Následující
křivka má dimenzi rovnu jedné, ale je zobrazována v trojrozměrném
prostoru:
| x |
= |
sin(t2)*log(t) |
(1.2) |
| y |
= |
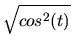 |
(1.3) |
| z |
= |
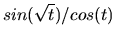 |
(1.4) |
Jediným použitým parametrem je zde opět t, polohu bodu potom definují
tři souřadnice x,y a z.
Také můžeme uvažovat tak, že pro křivky, které mají dimenzi jedna, je
definována jejich délka (která může být i nekonečná), ale jejich plocha
je nulová (jsou nekonečně tenké).
Jakákoliv hladká plocha (kruh, trojúhelník, n-úhelník) má dimenzi rovnu
2, to znamená, že poloha bodu musí být definována pomocí dvou
souřadnic. Například sedlová plocha je definována takto:
| x |
= |
u |
(1.5) |
| y |
= |
v |
(1.6) |
| z |
= |
u*v |
(1.7) |
kde u a v jsou parametry, které jednoznačně definují jakýkoliv bod
na ploše, zatímco x,y a z jsou výsledné souřadnice bodu v prostoru
pro dané u a v.
Takto definované plochy mají určitý obsah, ale jejich objem je nulový,
protože mají nulovou tloušťku.
Krychle, koule, válec nebo celý běžný prostor kolem nás mají
dimenzi 3, protože poloha bodu je v nich jednoznačně určena třemi
souřadnicemi.
Takto lze samozřejmě pokračovat dále, ale s dalšími dimenzemi
nemáme zkušenosti - možná ani neexistují. Z matematického
hlediska však není velkým problémem definovat například čtyřrozměrnou
kouli vzorcem:
Přitom x,y,z a w jsou polohy bodu v jednotlivých souřadných osách.
Zde je funkce pro čtyřrozměrnou kouli zapsána implicitně, to znamená, že
nejsou přímo vyjádřeny jednotlivé souřadnice, ale je pouze zapsána
podmínka pro jejich vzájemný vztah.
Trošku specifickým případem je bod, který má dimenzi 0, poněvadž polohu
bodu v něm samém není třeba určovat žádnou souřadnicí.
Ve všech předchozích případech jsme mluvili o dimenzi, která je
specifikována celým číslem. Tato dimenze se nazývá dimenze
topologická.
Pro tyto tělesa, která můžeme označit jako normální nebo
běžné, platí, že všechny jejich parametry mohou být zadány v
libovolné jednotce, aniž by se změnily vlastnosti tělesa. To znamená, že
nezáleží na měřítku, se kterým se na těleso díváme.
V klasické fyzice jsou tyto zákonitosti také využívány. Například při
výpočtu proudu protékajícího elektrickým obvodem můžeme napětí udávat v
kilovoltech, milivoltech nebo v jakékoliv jiné jednotce. To stejné
platí při udávání ohmického odporu rezistoru.




Next: Nekonečně členité útvary
Up: Fraktální geometrie
Previous: Definice fraktální geometrie
Tisnovsky Pavel
1999-05-30